Advanced Feature Attribution Techniques for Deep Learning Models

Deep learning models, particularly those in computer vision (CNNs, Vision Transformers), natural language processing (Transformers, xLSTM), and tabular data (MLPs, Gradient-Boosted Trees), have achieved remarkable performance across domains. However, their opaque decision-making processes, often referred to as the "black box" problem, pose significant challenges in high-stakes applications such as healthcare, finance, autonomous systems, and legal decision-making.

Explainable AI (XAI) seeks to demystify model predictions by providing human-interpretable insights into how inputs influence outputs.

While there are multiple dimensions of explainability, such as explaining via the input space, explaining by example (Nearest neighbor examples, prototypes, influence functions), explaining by concepts (Testing with Concept Activation Vectors, concept bottleneck models), or explaining model behaviour (partial dependence plots, SHAP values), this post focuses on advanced input space explanations.

Input space explanations aim to answer:

• Which parts of the input (pixels, words, features) were most influential in the model's decision?
• How do small perturbations in the input affect the output?
• Can we visualize or quantify the importance of input components?

Gradient-Based Techniques — Attribution via Backpropagation

Gradient-based methods exploit the differentiable nature of deep neural networks to compute how each input feature affects the output. These techniques are model-agnostic within differentiable architectures (CNNs, Transformers, MLPs) and provide fine-grained, pixel-level or token-level explanations.

Saliency Maps

Saliency maps compute the gradient of the output with respect to the input, highlighting regions where small changes would most significantly alter the prediction.

Intuitively, steep gradients indicate high sensitivity, meaning those input features are crucial for the decision.

Given an input $x$, a model $f$, and a target class $c$, the saliency map $S$ can be defined as:

$$S(x) = \left| \frac{\partial f_c(x)}{\partial x} \right|$$

where

• $f_c(x)$: Model’s confidence score for class $c$.
• $\frac{\partial f_c(x)}{\partial x}$: Gradient of the output w.r.t. the input.

Algorithm

1. Perform a forward pass to compute $f_c(x)$
2. Compute the gradient wrt. to the input $\nabla_x f_c(x)$ via backpropagation
3. Take the absolute value (or square) to measure magnitude

Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps

This paper addresses the visualisation of image classification models, learnt using deep Convolutional Networks (ConvNets). We consider two visualisation techniques, based on computing the gradient of the class score with respect to the input image. The first one generates an image, which maximises the class score [Erhan et al., 2009], thus visualising the notion of the class, captured by a ConvNet. The second technique computes a class saliency map, specific to a given image and class. We show that such maps can be employed for weakly supervised object segmentation using classification ConvNets. Finally, we establish the connection between the gradient-based ConvNet visualisation methods and deconvolutional networks [Zeiler et al., 2013].

arXiv.orgKaren Simonyan

Saliency Maps are simple and efficient methods to gain insight into any differentiable model, providing fine-grained importance scores on an input feature level.

On the other hand, Saliency Maps often suffer from gradient saturation, as deep networks often have near zero gradients due to ReLU/sigmoid activations. Additionally, Saliency Maps tend to be noisy as absolute gradients may highlight rather irrelevant high-frequency patterns.

Grad-CAM (Gradient-Weighted Class Activation Mapping)

Grad-CAM improves upon saliency maps by focusing on higher-level feature maps (e.g., last convolutional layer in CNNs) rather than raw input gradients.

It weights feature maps by their gradient importance and aggregates them into a coarse heatmap.

Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization

We propose a technique for producing “visual explanations” for decisions from a large class of CNN-based models, making them more transparent. Our approach - Gradient-weighted Class Activation Mapping (Grad-CAM), uses the gradients of any target concept, flowing into the final convolutional layer to produce a coarse localization map highlighting important regions in the image for predicting the concept. Grad-CAM is applicable to a wide variety of CNN model-families: (1) CNNs with fully-connected layers, (2) CNNs used for structured outputs, (3) CNNs used in tasks with multimodal inputs or reinforcement learning, without any architectural changes or re-training. We combine Grad-CAM with fine-grained visualizations to create a high-resolution class-discriminative visualization and apply it to off-the-shelf image classification, captioning, and visual question answering (VQA) models, including ResNet-based architectures. In the context of image classification models, our visualizations (a) lend insights into their failure modes, (b) are robust to adversarial images, (c) outperform previous methods on localization, (d) are more faithful to the underlying model and (e) help achieve generalization by identifying dataset bias. For captioning and VQA, we show that even non-attention based models can localize inputs. We devise a way to identify important neurons through Grad-CAM and combine it with neuron names to provide textual explanations for model decisions. Finally, we design and conduct human studies to measure if Grad-CAM helps users establish appropriate trust in predictions from models and show that Grad-CAM helps untrained users successfully discern a ‘stronger’ nodel from a ‘weaker’ one even when both make identical predictions. Our code is available at https://github.com/ramprs/grad-cam/, along with a demo at http://gradcam.cloudcv.org, and a video at youtu.be/COjUB9Izk6E.

arXiv.orgRamprasaath R. Selvaraju

For a CNN, let $A^k$ be the activation map of the $k$-th feature in the final convolutional layer. The Grad-CAM heatmap $L_{Grad-CAM}$ is:

$$L_{Grad-CAM} = \text{ReLU}\left( \sum_k \alpha_k A^k \right)$$

where the importance weight $\alpha_k$ is:

$$\alpha_k = \frac{1}{Z} \sum_i \sum_j \frac{\partial f_c(x)}{\partial A_{ij}^k}$$

• $Z$: Normalization constant (number of pixels).
• $\text{ReLU}$: Applied to keep only positive influences.

Algorithm

1. Perform a forward pass to get $f_c(x)$ and feature maps $A^k$.
2. Compute gradients $\nabla_{A^k} f_c(x)$ via backpropagation.
3. Global average pooling of gradients to get $\alpha_k$.
4. Weighted sum of feature maps, followed by ReLU.

Grad-CAM improves upon Saliency Maps by yielding less noisy attribution maps as it operates on higher-level features.

However, as the final heatmap is upsampled to the input size, some fine details are lost in the process, in turn it might miss small but critical features. Additionally, Grad-CAM is not applicable to fully connected layers but relies on convolutional feature maps.

Integrated Gradients

Gradient-based attribution methods often lack a clear baseline input for comparison, leading to arbitrary or incomplete explanations, a problem known as the reference problem.

Integrated Gradients (IG) fixes this by integrating gradients along a path from a defined baseline (e.g., zero input) to the actual input, ensuring the sum of attributions matches the difference between the model’s output and the baseline (completeness).

For input $x$ and baseline $x'$ (often zero), the attribution $A_{IG}$ is:

$$A_{IG}(x) = (x - x') \times \int_{\alpha=0}^1 \frac{\partial f(x' + \alpha (x - x'))}{\partial x} \, d\alpha$$

The integral is approximated via Riemann sums in practice.

Algorithm

1. Choose a baseline $x'$ (e.g., black image, zero embedding, ...)
2. Interpolate between $x'$ and $x$ in small steps
3. Compute gradients at each step and accumulate

Integrated Gradients works with any differentiable model, serves as a more robust alternative for the gradient saturation problem and can even give axiomatic guarantees, satisfying sensitivity (if a feature is essential, it will get non-zero attribution) and implementation invariance (same explanation for functionally equivalent models)

Axiomatic Attribution for Deep Networks

We study the problem of attributing the prediction of a deep network to its input features, a problem previously studied by several other works. We identify two fundamental axioms---Sensitivity and Implementation Invariance that attribution methods ought to satisfy. We show that they are not satisfied by most known attribution methods, which we consider to be a fundamental weakness of those methods. We use the axioms to guide the design of a new attribution method called Integrated Gradients. Our method requires no modification to the original network and is extremely simple to implement; it just needs a few calls to the standard gradient operator. We apply this method to a couple of image models, a couple of text models and a chemistry model, demonstrating its ability to debug networks, to extract rules from a network, and to enable users to engage with models better.

arXiv.orgMukund Sundararajan

Notably, computational cost is a weak point, as IG requires the calculation of multiple gradients, and even though it's guaranteed to highlight essential features, it still might highlight irrelevant features.

Input X Gradient

Input X Gradient is a simple but effective variant of Saliency Maps which multiplies the input by its gradient, emphasizing both the magnitude of the input and its gradient importance.

Input X Gradient Attribution $A_{\text{Input X Gradient}}$ is defined as

$$A_{\text{Input X Gradient}}(x) = x \odot \frac{\partial f_c(x)}{\partial x}$$

where $\odot$ denotes the element-wise (Hadamard) product.

Input X Gradient improves upon Saliency Maps, while still being simpler than other discussed techniques such as Integrated Gradients or Grad-CAM, however, it still suffers from gradient saturation and does not give theoretical guarantees like Integrated Gradients.

Gradient SHAP (Gradient SHapley Additive exPlanations)

Gradient SHAP merges SHAP (SHapley Additive exPlanations), a framework rooted in cooperative game theory that assigns fair feature contributions by computing Shapley values (the average marginal impact of a feature across all possible feature coalitions) with gradient-based approximations.

Instead of exhaustively evaluating all coalitions, it efficiently estimates Shapley values by sampling gradients along paths from a baseline input, blending SHAP’s theoretical rigor with the scalability of gradient methods.

The SHAP value for feature $i$ is:

$$\phi_i = \mathbb{E}_{x' \sim p(x')}\left[ \frac{\partial f(x')}{\partial x_i} \cdot (x_i - x'_i) \right]$$

where

• $p(x')$: Distribution over baseline inputs (e.g., mean, random samples).

Approximated via Monte Carlo sampling.

Gradient SHAP connects gradients to Shapley values and positions itself as a model-agnostic explainable AI technique, theoretically grounded in game theory.

Notably, it is however computationally quite intensive as it requires many gradient evaluations and assumes feature independence, which means it may fail if features are correlated.

DeepLIFT (Deep Learning Important FeaTures)

DeepLIFT computes neuron-level contribution scores by comparing the difference in activations between a given input and a reference input (e.g., baseline or neutral example).

Unlike gradient-based methods which rely on derivatives alone, DeepLIFT propagates contributions backward through the network, assigning credit to each neuron while explicitly addressing the gradient saturation problem. This neuron-centric approach ensures more reliable and meaningful attributions.

Learning Important Features Through Propagating Activation Differences

The purported “black box” nature of neural networks is a barrier to adoption in applications where interpretability is essential. Here we present DeepLIFT (Deep Learning Important FeaTures), a method for decomposing the output prediction of a neural network on a specific input by backpropagating the contributions of all neurons in the network to every feature of the input. DeepLIFT compares the activation of each neuron to its ‘reference activation’ and assigns contribution scores according to the difference. By optionally giving separate consideration to positive and negative contributions, DeepLIFT can also reveal dependencies which are missed by other approaches. Scores can be computed efficiently in a single backward pass. We apply DeepLIFT to models trained on MNIST and simulated genomic data, and show significant advantages over gradient-based methods. Video tutorial: http://goo.gl/qKb7pL, ICML slides: bit.ly/deeplifticmlslides, ICML talk: https://vimeo.com/238275076, code: http://goo.gl/RM8jvH.

arXiv.orgAvanti Shrikumar

For a neuron with input $x$ and output $y$, the contribution $C_{\Delta x \Delta y}$ is:

$$C_{\Delta x \Delta y} = \sum_{i,j} \frac{y - y_{ref}}{x_i - x_{i,ref}} \cdot (x_i - x_{i,ref})$$

where $y_{ref}$ is the output at reference input.

Contrary to the other explored methods, DeepLIFT handles gradient saturation better, however, it requires careful reference selection and is more complex to implement.

Layer-wise Relevance Propagation (LRP)

Layer-wise Relevance Propagation is gradient-inspired XAI technique, which explains neural network decisions by backward-passing relevance scores from the output to input features, ensuring the total relevance is preserved.

Unlike gradient-based methods, LRP uses layer-specific rules (e.g., for linear, ReLU, or pooling layers) to distribute importance proportionally to each neuron’s contribution.

LRP generates fine-grained explanations, showing which input regions most influenced the prediction.

While powerful, LRP’s quality depends on propagation rules, and its explanations may still reflect model biases.

For a layer $l$, the relevance $R$ is propagated as:

$$R_i^{(l)} = \sum_j \frac{a_i w_{ij}}{\sum_k a_k w_{kj}} R_j^{(l+1)}$$

where

• $a_i$: Activation of neuron $i$.
• $w_{ij}$: Weight from $i$ to $j$.
• $R_j^{(l+1)}$: Relevance of neuron $j$ in the next layer.

LRP is well-suited for complex architectures, including convolutional neural networks (CNNs) and multi-layer perceptrons (MLPs). It delivers fine-grained, pixel-level interpretability without relying on gradient calculations, instead leveraging activation patterns and network weights to generate explanations.

However, its effectiveness depends heavily on the chosen propagation rules, as different variants can yield inconsistent or conflicting results. Compared to approaches like attention mechanisms or gradient-based methods, the explanations it produces may also feel less intuitive or harder to interpret.

Attention-Based Techniques — Leveraging Model-Inherent Focus

Attention mechanisms provide a natural way to interpret model decisions by highlighting which parts of the input the model focuses on at each step. While not always faithful, attention weights offer intuitive and efficient explanations.

Self-Attention Visualization

In Transformer models (BERT, ViT, LLMs), self-attention weights indicate how much each token (or patch) attends to every other token. By visualizing these weights, we can see which input elements influence each other.

For a single attention head, the attention weights $A$ are:

$$A = \text{softmax}\left( \frac{Q K^T}{\sqrt{d_k}} \right)$$

where

• $Q$: Query matrix (from input embeddings)
• $K$: Key matrix
• $d_k$: Dimension of key vectors

Algorithm

1. Extract attention weights from a trained Transformer
2. Average across heads (or analyze per head)
3. Visualize as a heatmap (for text) or image overlay (for Vision Transformers)

Visualizing self-attention poses itself as an attractive feature attribution technique as it requires no additional computation (uses existing model weights), feels very intuitive, especially with the "attention" framing and works for multi-model models (e.g. CLIP or DALL-E).

However, as also noted in literature, Attention != Causation, hence attention visualizations are not necessarily faithful as the model may use the retrieved weights differently than only would expect. In addition, the multi-head attention is not guaranteed to learn patterns which make sense to be interpreted on their own or in combination with others, hence can be hard to interpret.

Attention Rollout

Since self-attention is recursive, Rollout aggregates attention weights across all layers to show long-range dependencies. It computes a joint attention graph by multiplying attention matrices sequentially.

For $L$ layers, the cumulative attention $R$ is:

$$R = A^{(1)} \cdot A^{(2)} \cdot \ldots \cdot A^{(L)}$$

where $A^{(l)}$ is the attention matrix at layer $l$.

Attention rollout effectively models complex relationships between tokens, offering a richer and more accurate representation than shallow (single-layer) attention mechanisms.

However, the model suffers from a combinatorial explosion of possible attention paths, making computation inefficient. Additionally, interpreting and visualizing attention patterns becomes increasingly difficult as sequence length grows.

Attention Gradients

While attention weights show where the model looks, attention gradients reveal how important those weights are for the final prediction. This combines attention and gradient-based methods.

The importance of attention weight $A_{ij}$ is:

$$I_{ij} = A_{ij} \cdot \frac{\partial f(x)}{\partial A_{ij}}$$

This approach offers a more accurate representation of attention compared to raw attention mechanisms by incorporating gradient-based importance. Additionally, it is highly versatile, as it can be applied to any model that relies on attention mechanisms.

One major drawback is its high computational cost, since it requires backpropagation through the attention components. Furthermore, while it improves upon traditional methods, it is not flawless and may still overlook certain dependencies in the data.

Permutation-Based Techniques — Measuring Impact via Perturbations

Unlike gradient or attention methods, permutation-based techniques measure importance by observing how output changes when input features are perturbed. These are model-agnostic and work even for non-differentiable models (e.g., Random Forests, Gradient-Boosted Trees).

LIME (Local Interpretable Model-agnostic Explanations)

LIME explains a single prediction by fitting a simple, interpretable model (e.g., linear regression) to perturbed versions of the input. The feature weights in this local model serve as explanations.

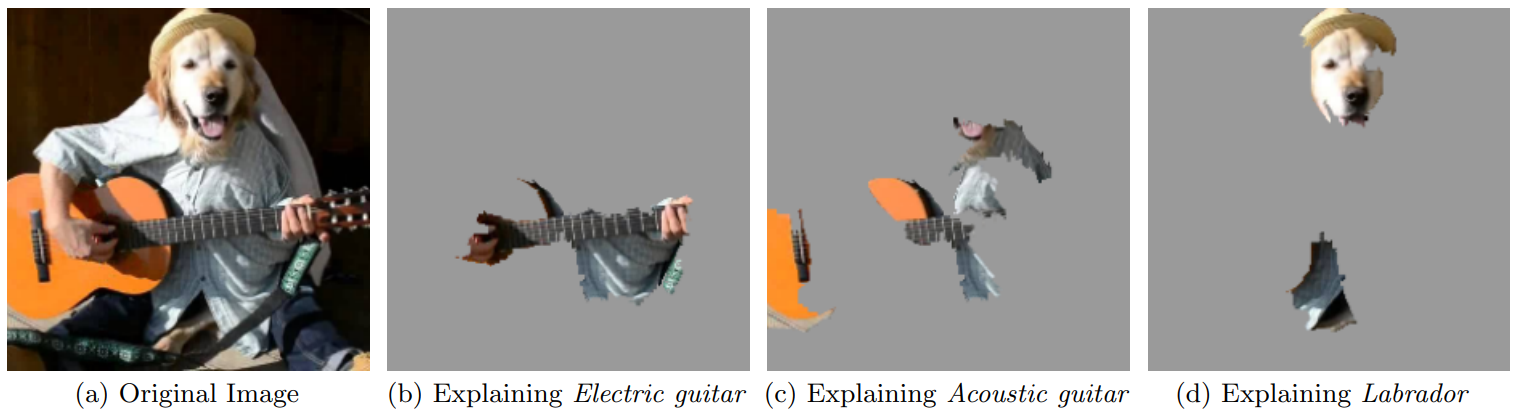
Algorithm

1. Generate perturbed samples $x'$ around $x$ (e.g., by randomly masking words in text or superpixels in images).
2. Get predictions $f(x')$ for perturbed samples.
3. Fit a weighted linear model $g$ to approximate $f$ locally:

$$g(z) = w_0 + \sum_i w_i z_i$$

where

• $z$: Binary vector indicating presence/absence of features.
• $w_i$: Explanation weights (importance of feature $i$).

“Why Should I Trust You?”: Explaining the Predictions of Any Classifier

Despite widespread adoption, machine learning models remain mostly black boxes. Understanding the reasons behind predictions is, however, quite important in assessing trust, which is fundamental if one plans to take action based on a prediction, or when choosing whether to deploy a new model. Such understanding also provides insights into the model, which can be used to transform an untrustworthy model or prediction into a trustworthy one. In this work, we propose LIME, a novel explanation technique that explains the predictions of any classifier in an interpretable and faithful manner, by learning an interpretable model locally around the prediction. We also propose a method to explain models by presenting representative individual predictions and their explanations in a non-redundant way, framing the task as a submodular optimization problem. We demonstrate the flexibility of these methods by explaining different models for text (e.g. random forests) and image classification (e.g. neural networks). We show the utility of explanations via novel experiments, both simulated and with human subjects, on various scenarios that require trust: deciding if one should trust a prediction, choosing between models, improving an untrustworthy classifier, and identifying why a classifier should not be trusted.

arXiv.orgMarco Tulio Ribeiro

LIME is highly versatile, as it can be applied to any type of classifier without modification. Its explanations are intuitive and easy for humans to grasp, thanks to the simplicity of the underlying linear model. Additionally, it is adaptable across different data types, including text, images, and structured tabular data, making it widely applicable in various domains.

However, the explanations produced can be inconsistent, as they heavily rely on the chosen perturbation approach during analysis. The technique also becomes computationally expensive when dealing with high-dimensional data, such as images, due to the increased processing demands. Furthermore, it tends to focus on local behavior, which means it may overlook broader, global patterns in the data that could provide deeper insights.

Occlusion Sensitivity

Occlusion sensitivity systematically hides (occludes) parts of the input and measures how much the prediction changes. Regions causing large drops in confidence are deemed important.

Algorithm

1. Slide a mask (e.g., gray patch for images, [MASK] for text) over the input.
2. Record the change in prediction confidence.
3. Generate a heatmap of importance scores.

This approach is straightforward and easy to use, requiring no gradient calculations, making it compatible with any model. Additionally, it can be applied to various different data types, including images and text.

Unfortunately, it demands significant computational resources due to repeated forward passes. The choice of mask size can impact performance, as overly large or small masks may overlook important details, and additionally, it may struggle to detect intricate feature interactions.

SHAP (SHapley Additive exPlanations)

SHAP (SHapley Additive exPlanations) explains machine learning predictions by assigning each feature a Shapley value, a concept from game theory that fairly distributes credit among contributors. For a given feature, SHAP calculates its average impact on the model’s output by considering all possible feature coalitions (subsets of features that either include or exclude it).

A feature coalition is simply any combination of features working together. For example, if a model uses features $\text{A}$, $\text{B}$, and $\text{C}$, coalitions could be $\{\text{A}\}$, $\{\text{B}, \text{C}\}$, or even the empty set $\{\}$. SHAP measures how much adding a specific feature (e.g., $\text{A}$) changes the prediction when combined with every possible coalition of the remaining features.

The SHAP value for feature $i$ is:

$$\phi_i = \sum_{S \subseteq F \setminus \{i\}} \frac{|S|! (|F| - |S| - 1)!}{|F|!} \left( f(S \cup \{i\}) - f(S) \right)$$

where

• $F$: Set of all features.
• $S$: Subset of features excluding $i$.
• $f(S)$: Model prediction with features in $S$.

SHAP is theoretically robust, providing a unique, fairness-guaranteed solution. Additionally, it’s model-agnostic, meaning it works with any ML algorithm while maintaining consistency.

However, it struggles with high-dimensional data due to computational costs. It also assumes independent features, which can lead to unreliable results when variables are correlated.

Some Open Challenges

While explainable AI (XAI) has made substantial strides in recent years, it remains an unsolved challenge with critical open questions. Researchers and practitioners continue to grapple with fundamental limitations that hinder the development of truly transparent and trustworthy AI systems.

Faithfulness vs. Plausibility

One of the most pressing issues in XAI is the tension between faithfulness (whether an explanation accurately reflects the model’s decision-making process) and plausibility (whether the explanation appears reasonable to humans).

Many widely used techniques, such as attention mechanisms in deep learning, often generate interpretations that seem intuitive but may not faithfully represent the model’s inner workings. For instance, an attention heatmap might highlight certain words in a text, but this does not necessarily mean those words were the true drivers of the prediction.

To address this gap, robust evaluation frameworks are essential. Perturbation-based tests (e.g., removing or altering input features to observe changes in output) and controlled human studies can help assess whether explanations are both faithful and meaningful.

Scalability

Another major hurdle is the computational inefficiency of many XAI methods when applied to large-scale models, particularly modern deep learning systems like large language models (LLMs) with billions of parameters. Techniques such as SHAP (SHapley Additive exPlanations) and LIME (Local Interpretable Model-agnostic Explanations), while powerful, become prohibitively expensive as model size grows.

Conclusion

As AI systems become more complex and high-stakes, the demand for rigorous, faithful, and actionable explanations will only grow. Future advancements in neurosymbolic AI, causal reasoning, and human-AI collaboration will further bridge the gap between model opacity and human understanding.